We provide wide range of electronic components to meet your specific needs, which are helpful for your value added products and solution businesses.

As electronic devices become more compact and components increasingly integrated, heat density rises. This means effective thermal management is essential to the design of devices and its components.

What is Thermal Design?

This involves using heat dissipation materials to manage the heat generated within electronic devices and/or reducing component temperatures by transferring heat to a cooling surface, such as the device casing.

Why is Thermal Design necessary?

Electronic components mounted on PCBs in many devices generate heat when electricity flows through them, leading to various issues as listed below. Effective thermal design is essential to address these challenges.

1. Functional Issues：Such as hortened component lifespan due to electronic components becoming very hot
2. Mechanical Issues：Such as damage to components due to thermal expansion or chemical changes 　　　　　　　　　　　　　
3. User Safety Issues： Such as burns due to high touch temperature

Fundamentals of Heat Transfer

There are three modes of heat transfer.

1. Thermal Conduction: the process by which heat transfers within a solid
   Ex: When the tip of a spoon is heated over fire, the part being held in hand also becomes hot.
2. Convection Heat Transfer: The process in which heat is transferred to a fluid (such as air or liquid) in contact with a heated object.
   Ex: When a frying pan is heated on a gas stove, the air above it warms up due to heat transfer.
3. Thermal Radiation: The transfer of thermal energy through electromagnetic waves emitted by matter.
   Ex: Sunlight. The heat from the sun is not carried by air but travels through the vacuum of space as electromagnetic radiation.

Thermal design is implemented with careful consideration of these heat transfer mechanisms.

Thermal Conductivity and Thermal Resistance

Fourier's Equation: Q=λ×((ΔT・S)/d)
Q: net heat transfer (W), λ: thermal conductivity (W/m･K), ΔT: temperature difference, S: cross-sectional area,
d: distance

1. Thermal conductivity: a material's ability to conduct heat
   This value is a constant and remains unchanged even when there are changes to its surrounding environment.
   λ (Thermal Conductivity) = (Q・d)/(ΔT・S)
   * (d/ΔT = constant)
2. Thermal resistance: a measure of how well a material resists heat flow
   This value varies depending on the distance from the heat source, contact degree, and area, even with the same thermal pad.
   Thermal resistance becomes smaller with a larger area, higher thermal conductivity, and shorter distance (thinner thickness).
   R1 (Thermal Resistance): °C/W = d/(λ・S)

The above properties are important for thermal design.

Our Thermal Evaluation Method

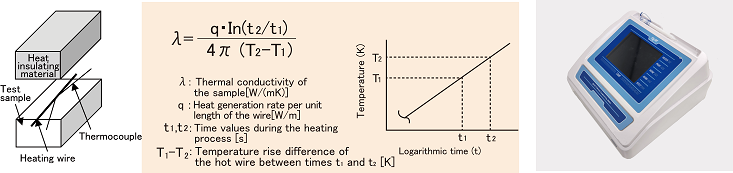
Thermal conductivity 1 (JIS R 2616 Hot-wire method)

A thin heating wire (hot wire) is embedded in the test sample, and a constant electric current is applied to generate heat.
The temperature rise around the hot wire depends on the thermal conductivity of the sample. When plotted with a logarithmic time scale, the temperature increase appears as a straight line, as shown in the figure below.
The slope of this line is inversely proportional to the thermal conductivity of the sample: a sample with low thermal conductivity will produce a steeper slope, while a sample with high thermal conductivity will result in a gentler slope.
In other words, the thermal conductivity of the sample can be determined from the slope of the temperature rise curve plotted against logarithmic time.

Thermal conductivity 2 (ISO22007-2 Hot Disk method)

By applying a constant current to the Hot Disk sensor, it generates heat. During this process, the change in voltage across the sensor is measured.
From the applied current and the measured voltage change, the electrical resistance of the Hot Disk sensor can be determined, allowing the temperature change of the sensor over time to be calculated.

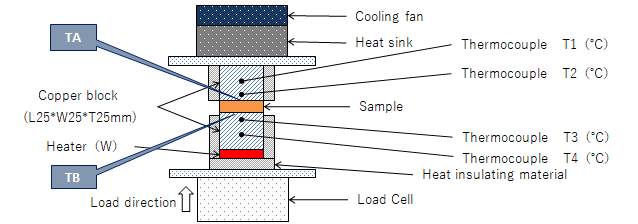
Thermal Resistance (ASTM D5470 compliant)

Using the sample's temperature difference between top (TA) and bottom (TB) and net heat transfer (Q), thermal resistance can be calculated following the equation.
Thermal Resistance= (TA−TB)/Q

TA: Temperature of the sample and contact surface on the upper copper block
　　(calculated from the temperature and distance at two points on the upper copper block, T1 and T2)
TB: Temperature of the sample and contact surface on the lower copper block
　　(calculated from the temperature and distance at two points on the lower copper block, T3 and T4)

Advantages of using thermal pad (vs thermal grease)